Aidan Mason-Mackay: MRI, circumventing the rules I learnt in my physics degree

I was introduced to MRI when I started my PhD, and I was fascinated to learn that it circumvents two so-called rules I’d learnt during my undergraduate degree in physics. I’ll share the first one with you here, and the other in my next blog post. I hope these posts will give you more appreciation for this genius technology that lets us see what’s going on inside our brains and bodies.

Here’s something you need to know before we start. Most medical imaging works by sending waves at an object and then measuring them once they’ve made their way back out of that object. The waves that come back contain the information needed to make an image of your head or knee, or whatever else your doctor wants to see.

Most physicists are well-versed with a rule, stemming from ‘Heisenberg’s uncertainty principle’, that the resolution of your image can’t exceed the wavelength of the wave used to probe it.

X-rays (good for spotting broken bones) have wavelengths on the nanometer scale, and ultrasound waves (good for seeing unborn babies) have wavelengths on the micrometer scale. But MRI uses radio frequency waves, which are on the scale of meters. Despite this massive wavelength, MRI can achieve resolutions of less than a millimeter. Heisenberg’s uncertainty principle doesn’t limit MRI the way it does other imaging modalities, because MRI works in a unique way.

Instead of aiming waves at an object then seeing what comes back out, MRI deals with some more mind-bending concepts from quantum mechanics. In short, it first magnetizes your body, then sends some waves to disrupt this magnetization a little, then finally measures the waves that come back while the magnetization recovers from the disruption. During this recovery time, we manipulate the signals coming back so that they interfere – some get destroyed and others are amplified. This means we end up measuring something called the ‘k-space’ or ‘Fourier transform’ of the image. You can see a picture of a k-space below, as well as the image it can be turned into.

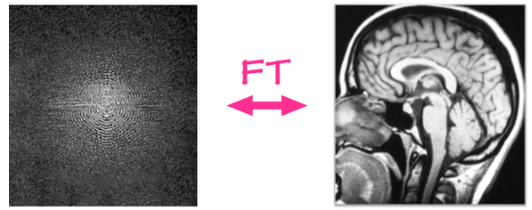
The concept behind k-space is that images can be created by adding together combinations of pictures of wave patterns. The k-space data tells us how much we need of each wave pattern to make the final image. This idea is better explained in pictures, so take a look at the image below, which shows images of waves being added together to create 1D and 2D images:

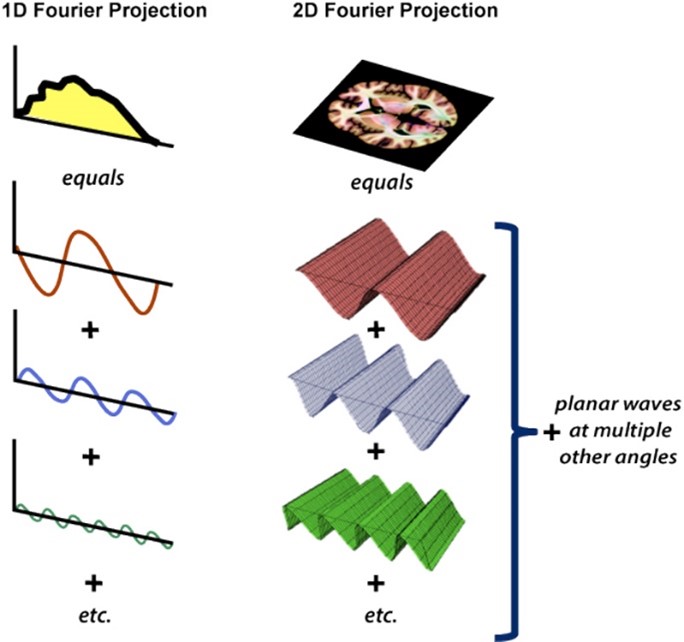
It’s impressive that MRI has managed to circumvent the resolution-limits imposed by Heisenberg’s uncertainty principle. It was a big surprise to me, given how much these limits were drilled into me during my undergraduate days. The idea is so novel and useful that a Nobel prize were awarded for it in 2003.

I hope that what you read made at least a little sense and gave you some more appreciation for the magic of MRI. In the next post, we’ll look into how MRI can be used to create not just images, but movies. And how, while creating these movies, we can break another rule that was drilled into me at university.

Aidan Mason-Mackay works as a doctoral researcher in the Neuro-Innovation PhD programme. His research focuses on improving the time resolution of functional MRI.