Aidan Mason-Mackay: High Resolution MRI, Where Abstract Maths Meets the Real World

In my last post, we discussed the physics of MRI, and one of two laws of physics that it circumvents. This time, we’ll explore the second of these rules, which allows us to make high-frame-rate videos of the brain. This post highlights the work of four mathematicians, who used abstract mathematics to make a big impact in the real world.

Firstly, why do we want these high-frame-rate videos? One of many reasons is to help us understand how memories are “saved” or consolidated in the brain. Understanding memory consolidation may help advance medicine, for example by giving insight into how and why people develop dementia.

The (over-simplified) working theory is that new memories are “saved” to short-term storage in the hippocampus (a sea-horse-shaped structure, deep in the brain) during the day. While we sleep, they get passed on to the neo-cortex (a set of layers in the outer area of your brain), for long-term storage. These memory-saving events happen very quickly, and a lot of the details are still unknown to scientists. We need high-frame rate videos of the brain so that we can see what’s going on.

We can make these videos using functional MRI or fMRI. It takes energy to think, and so our blood delivers extra oxygen to active areas of the brain. We can see changing blood oxygen levels in fMRI scans and use that information to infer what neurons are doing within the brain. If we get someone to sleep in an MRI machine, we might be able to witness their memories being saved.

The problem is that it takes a couple of seconds to collect enough MRI data to create a single image of the brain, and that limits our frame rate. We won’t see activity that happens within those seconds, and likely we’ll miss out on seeing the memories being saved. We need a bit of mathematics to understand and circumvent this limit.

The minimum data required to make an MRI image is governed by a rule called the Nyquist-Shannon sampling theorem. The idea is that, when measuring waves, like we do in MRI (see the last post), you need a minimum of two data points per wavelength. This rule is well-known to any physics undergraduate student, and for a long time it was considered unbreakable. Until the early 2000’s. In 2004, a group of four mathematicians started publishing papers on a new idea called compressed sensing. They were able to prove that, under certain conditions, the Nyquist-Shannon sampling limit could be broken.

The schematic below illustrates the power of what they proved. On the left, you can see that, if we collect enough data to satisfy the Nyquist-Shannon sampling theorem, we can create a nice image using the so-called Inverse Fourier Transform (see my last post).  On the right, we collect 4x less data, allowing us to achieve a 4x faster frame rate. The inverse Fourier Transform is failing us, but if we used compressed sensing, we can still get a nice image!

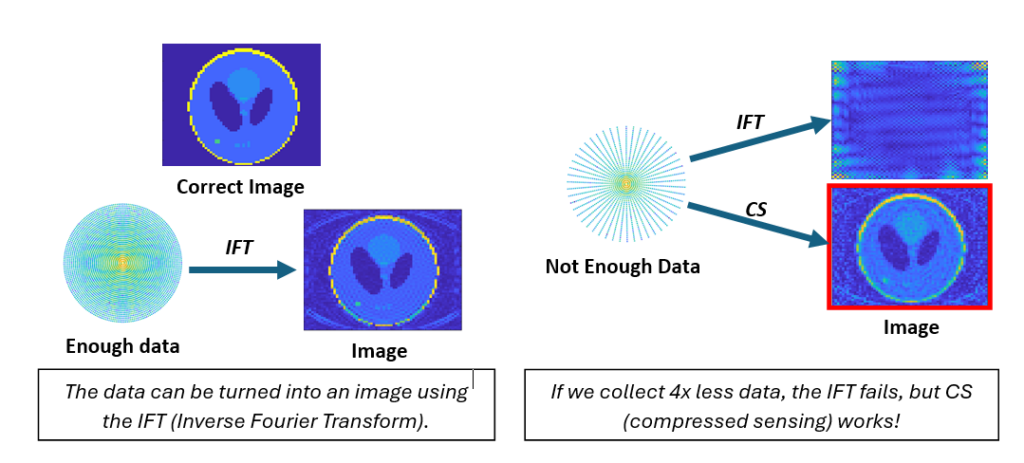
A detailed account of compressed sensing is beyond the scope of this post, but feel free to explore its Wikipedia page, Compressed sensing – Wikipedia. As is characteristic of any mathematical result, the impact of compressed sensing isn’t confined to any one discipline like MRI. It’s used all over the place, including, for example; image processing; astronomy; and computer science.

The utility of abstract maths hasn’t always been clear to me, and I was excited to come across this example where it makes its impact in the real world. Compressed sensing theory managed to circumvent a fundamental law of physics that I was taught as a student. It’s proved hugely useful to my research, and I hope it was interesting to learn about!

Aidan Mason-Mackay works as a doctoral researcher in the Neuro-Innovation PhD programme. His research focuses on improving the time resolution of functional MRI.