Melina Estela Dalmau: Thinking (and transforming) inside the box 

Most of us will have a brain scan at least once in our lives. 

The reasons can be quite varied: after a concussion, to check for internal bleeding or swelling; due to sudden numbness on one side of the body, to detect a possible stroke or tumor; or as a result of memory problems, indicating for example the onset of a neurodegenerative disease. So, a single brain scan (which results in a 3d brain image) is really powerful in providing information about a person’s brain health at a given point in time. I myself had a brain scan last year—fortunately not because I fell off my bike, but as a volunteer in a research project. 

In other cases, people might need not just one, but several brain scans over their lifes. And this opens the possibility to track brain anatomical changes of a person over time. Changes due to a disease, ageing or as a result of some treatment.  

From the research perspective, a next question could be: what if we combine brain scans from different people? Because then, we might notice generic patterns across people! Patterns related to specific diseases, ageing itself, or differences in treatment response based on gender. 

But just like apples can be more or less symmetric, bigger or smaller, the same goes for our brains. So in order to compare brain images effectively, we need a crucial step: image registration. 

What’s image registration? 

It’s the process of aligning images to a common coordinate space. We can think of this common space as a fixed, predefined box. Inside this box, we aim to tightly fit all brains under study (well, not the brains per se, but the 3d brain images acquired). However, since the box has fixed dimensions, some brains may not perfectly fit inside, or they may exceed its dimensions. And that’s where transformations come in. 

There are three types of transformations we can do: rigid, affine and nonlinear. Let’s see how we use them. 

Rigid transformations 

As the name says, they are rigid, meaning they preserve the size and shape of the image being transformed. In our case, the first rigid transformation needed is a translation, that is, shifting the brain images to the center of the box. Next, since each person rests their head in slightly different positions during a brain scan, we may need a rotation of the brain images to correct for these variations. 

Affine transformations 

Leaving behind rigidity, we have affine transformations. Those will make the brain images fit tightly in the box. It can be done through scaling, which is stretching or compressing the image in all directions; or through shearing, which stretches the image along one specific direction. Nitpicking note: parallel lines remain parallel after an affine transformation. 

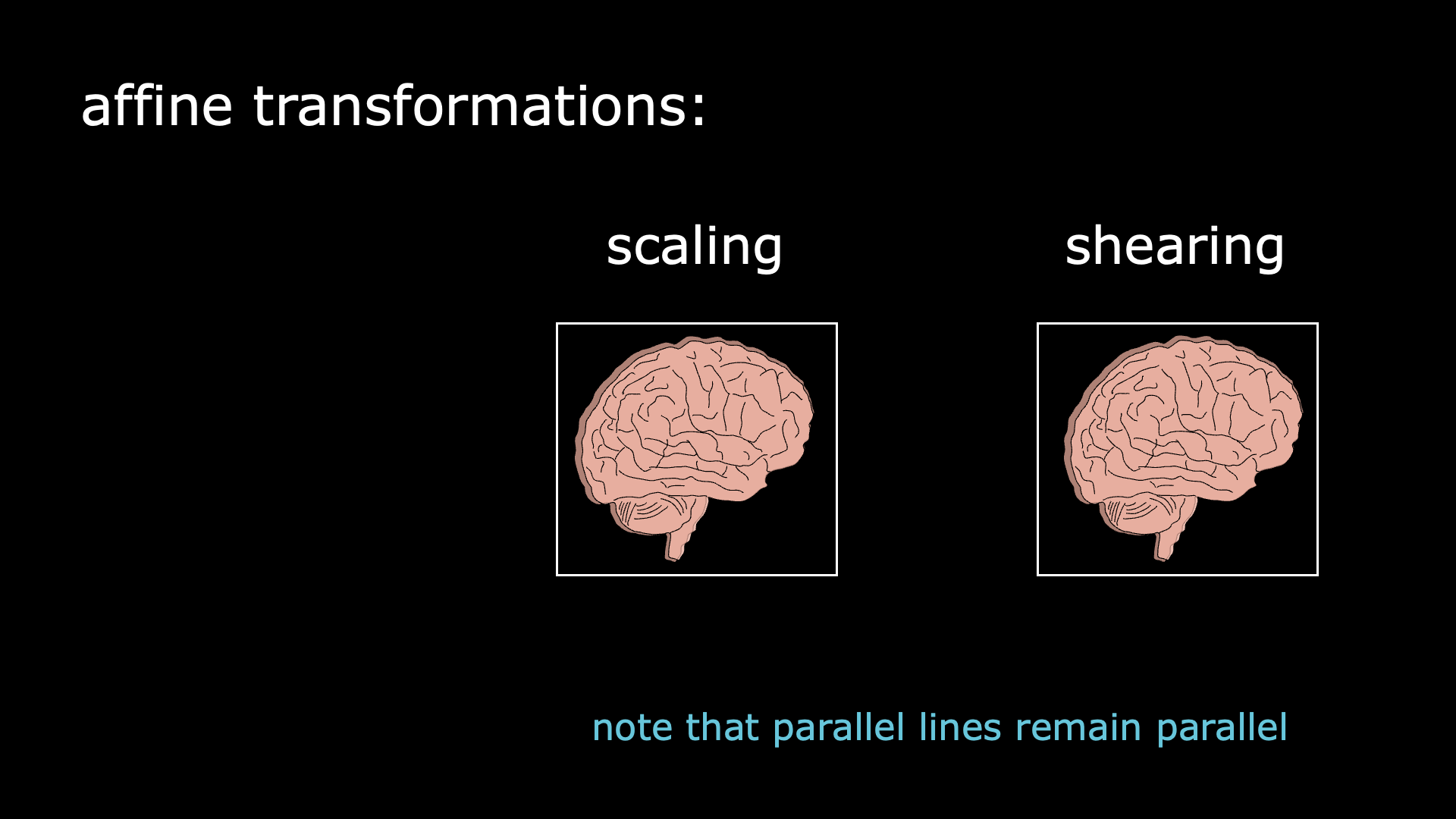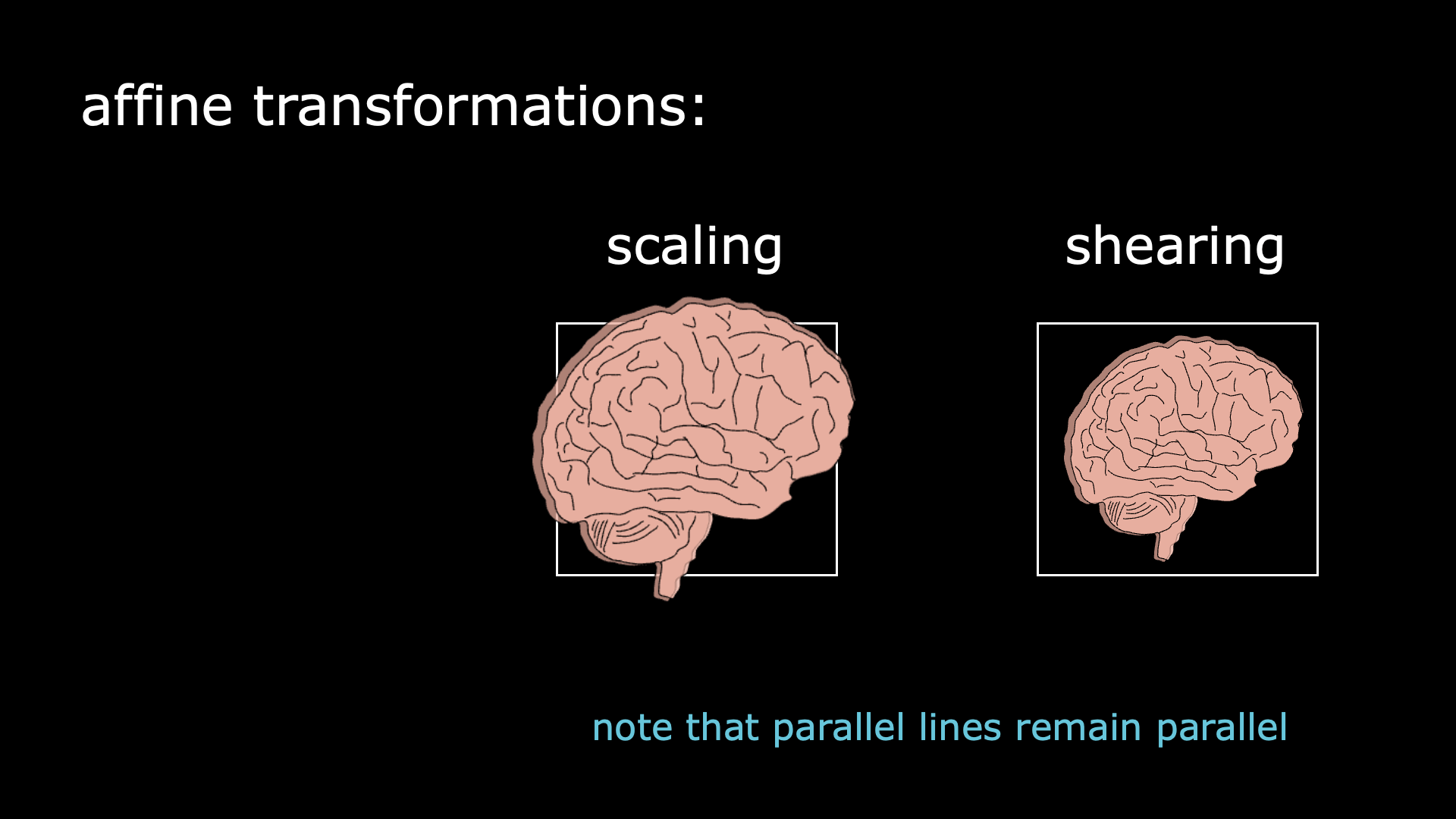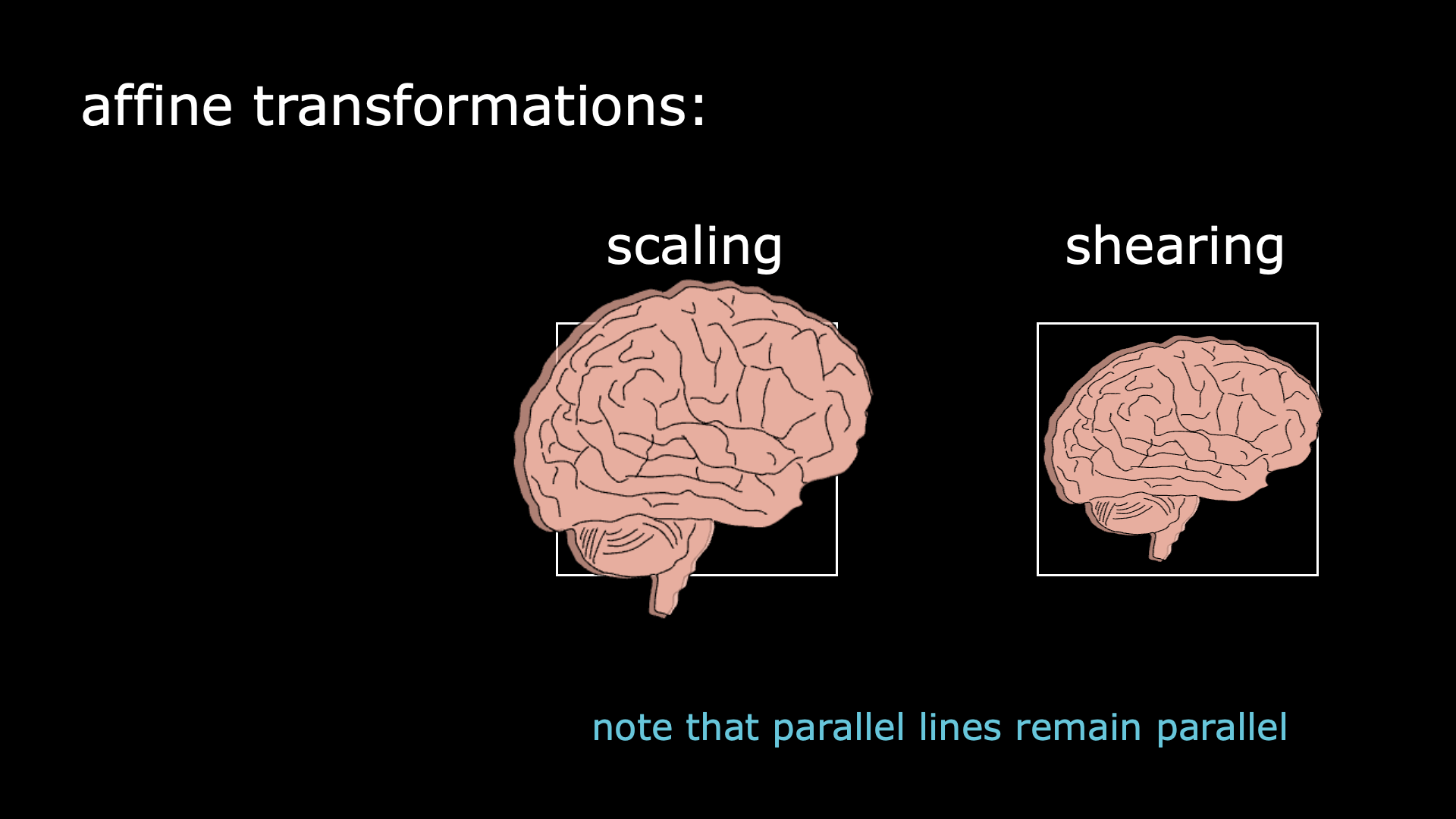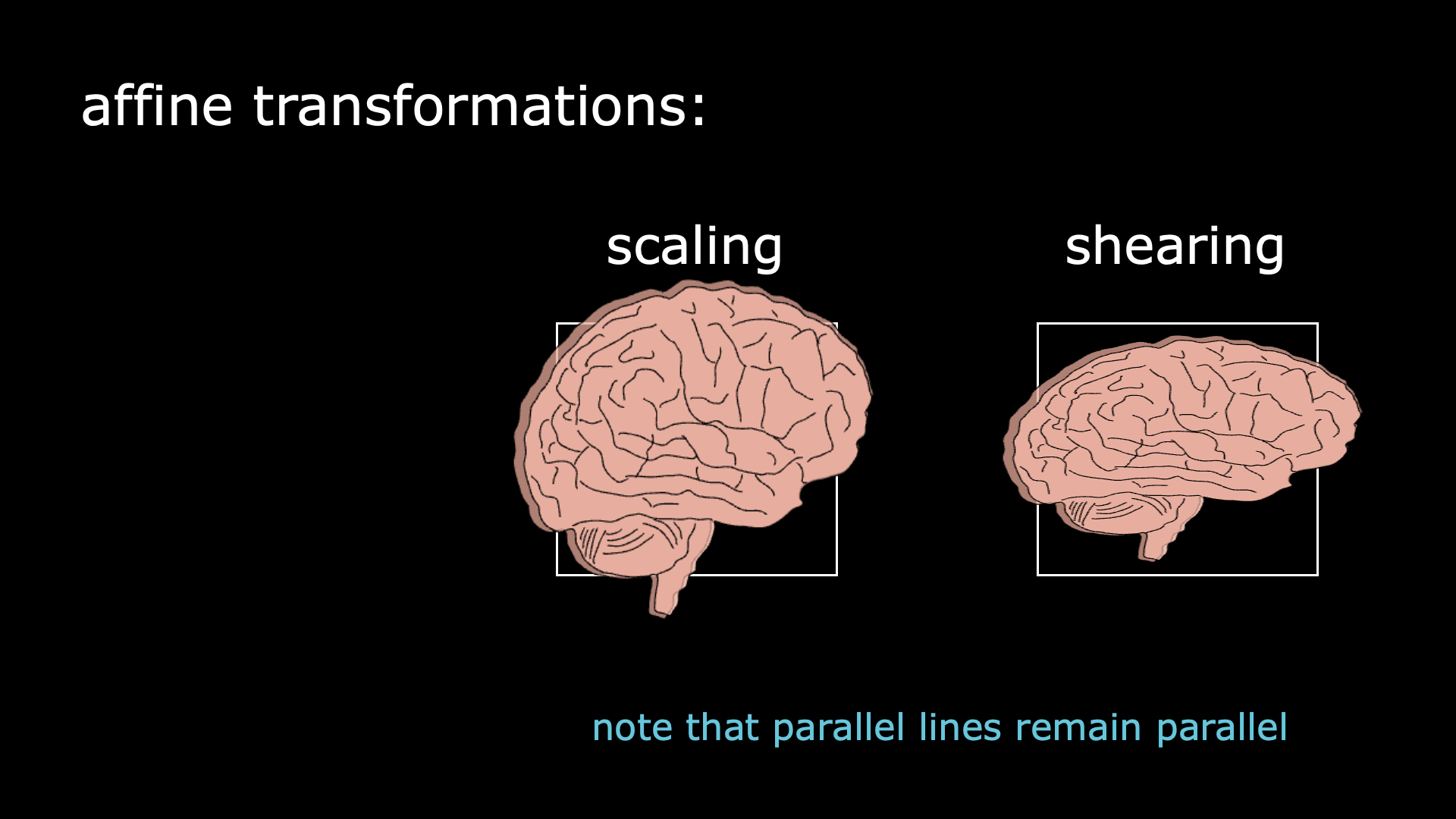
Nonlinear transformations 

With all the previous transformations, the brain images might still not be fitting perfectly in the box. Human brains have plenty of folds, and despite similarities, every single person has a uniquely shaped brain. By registering  the images to a common space (the box), we are smoothing out these individual anatomical differences to make them comparable.  

For this fine tuning, we need non-linear transformations. Non-linear because the changes are not applied to the image as a whole, but the changes are local. Said otherwise, different parts of the image will be adjusted independently, allowing for a more precise alignment of brain structures across people. As a note, with non-linear transformations parallel lines no longer remain parallel. 

That was a lot of theory! But with the next image everything will make sense. The first row shows 5 different brains scanned, the second row shows those same brains after applying linear transformations (i.e. rigid and affine), and the last row shows them after nonlinear transformations. 

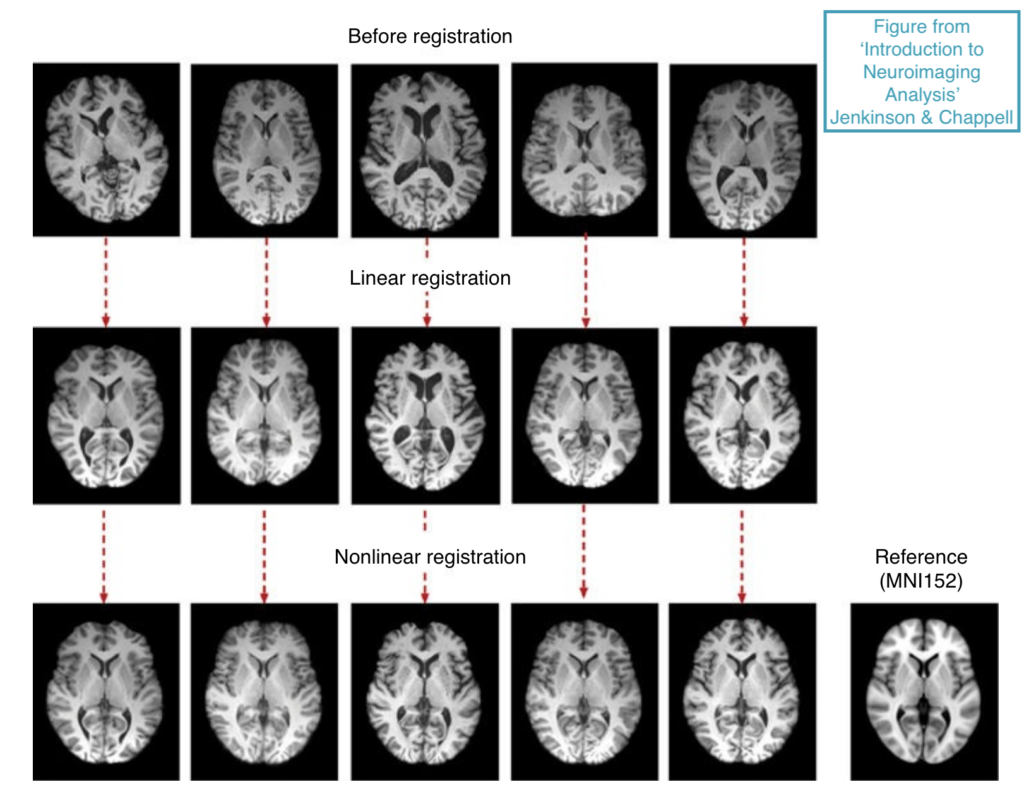
If we compare the first brain before and after registration (first column), we can clearly see that a rotation was needed for alignment. The brain in the third column has remarkably larger ventricles (those darker regions in the middle of the brain, which are the containers of the cerebrospinal fluid). In this case, the ventricles’ size has been adjusted through nonlinear transformations. Lastly, looking at the fourth column, I would emphasize how the brain shape has changed after registration. Indeed, we all have unique brain shapes! And by registering them, we smooth out these differences, enabling for more robust comparisons. 

You might have noticed that in the bottom-right corner of the last image it says “Reference (MNI 152)”. That’s the “box” (or common coordinate space) I’ve been refering to when describing the transformations. In practice, we don’t fit the brains into a predefined box, but into a brain template. In particular, “MNI 152” refers to a brain template made at the Montreal Neurological Institute averaging 152 brain scans from healthy young people. This template is widely used, but it’s not unique.  

Can we all fit into the same brain template? Definitely not. We cannot use the same reference to compare children’s brains to adult ones, or to study individuals with neurodegenerative conditions. That’s why researchers have developed templates for specific groups, since the choice of brain template depends on factors like age, gender, brain asymmetry, and disease specificity. This allows the extraction of patterns related to those group specificities. 

So overall, fitting into a box can be useful sometimes. However, don’t stay long inside it if you want to move forward. 

References 

Introduction to Neuroimaging Analysis, Jenkinson and Chappell, 2018. 

Evans et al. Brain templates and atlases. NeuroImage, 2012. 

Melina Estela Dalmau works as a doctoral researcher in the Neuro-Innovation PhD programme. Her research seeks to bridge the gap between imaging and brain tissue.