Coherence photonics

The growing interest towards ever more sophisticated optical systems in modern photonics has invoked the need for a full three-dimensional (3D) polarization treatment of light. For such genuinely 3D polarization states the local electric field evolves in three orthogonal directions in space. Light of this type is encountered, e.g., in optical near fields, tightly focused beams, and complex-structured electromagnetic radiation. Our research on random 3D optical fields has led to several discoveries concerning their polarimetric and dimensional structures, nonregular and anisotropic properties, as well as spin angular momentum characteristics, entailing new physical insights and notions about polarization of random light and with applications in high-numerical-aperture and nanophotonic systems. The research contains collaboration with the University of Zaragoza (Spain) as well as Shandong Normal University and Soochow University (China).

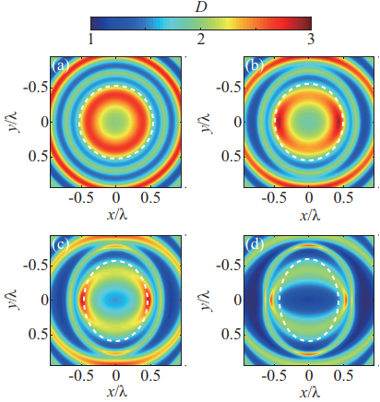
Distribution of the polarimetric dimension D in the focal plane of a tightly focused, partially polarized beam with the degree of polarization a) 0, b) 0.3, c) 0.6, and d) 0.9. Inside the dashed circle the intensity is larger than 10 % of its maximum value (from [7]).

Contact persons:
Asst. Prof. Andreas Norrman
Prof. Tero Setälä
Prof. Ari T. Friberg

1. A. Norrman, A. T. Friberg, J. J. Gil, and T. Setälä, “Dimensionality of random light fields”, J. Eur. Opt. Soc.-Rapid Publ. 13, 36 (2017).
2. J. J. Gil, A. Norrman, A. T. Friberg, and T. Setälä, “Polarimetric purity and the concept of degree of polarization”, Phys. Rev. A 97, 023838 (2018).
3. J. J. Gil, A. Norrman, A. T. Friberg, and T. Setälä, “Nonregularity of three-dimensional polarization states”, Opt. Lett. 43, 4611 (2018).
4. A. Norrman, J. J. Gil, A. T. Friberg, and T. Setälä, “Polarimetric nonregularity of evanescent waves”, Opt. Lett. 44, 216 (2019).
5. J. J. Gil, A. Norrman, A. T. Friberg, and T. Setälä, “Intensity and spin anisotropy of three-dimensional polarization states”, Opt. Lett. 44, 3578 (2019).
6. J. J. Gil, I. San José, A. Norrman, A. T. Friberg, and T. Setälä, “Sets of orthogonal three-dimensional polarization states and their physical interpretation”, Phys. Rev. A 100, 033824 (2019).
7. Y. Chen, F. Wang, Z. Dong, Y. Cai, A. Norrman, J. J. Gil, A. T. Friberg, and T. Setälä, “Polarimetric dimension and nonregularity of tightly focused light beams”, Phys. Rev. A 101, 053825 (2020).
8. J. J. Gil, A. Norrman, A. T. Friberg, and T. Setälä, “Effect of polarimetric nonregularity on the spin of three-dimensional polarization states”, New J. Phys. 23, 063059 (2021).
9. Y. Chen, F. Wang, Z. Dong, Y. Cai, A. Norrman, J. J. Gil, A. T. Friberg, and T. Setälä, “Structure of transverse spin in focused random light”, Phys. Rev. A 104, 013516 (2021).

Optical near fields: The manipulation and utilization of optical near fields at subwavelength dimensions play a vital role in nanophotonics. The celebrated surface plasmon polariton (SPP), in particular, has even triggered the rise of plasmonics as an own separate field covering multidisciplinary science and engineering. To date, however, most near-field investigations have concerned monochromatic and thus fully coherent fields, while in practice thermal effects, surface roughness, material impurities, and source fluctuations inevitably render the near field partially coherent. The rigorous assessment of coherence in such random optical near fields lies in our research focus. On the other hand, there is now a solid recognition that coherence also provides a novel and versatile degree of freedom to control the physical properties of optical near fields. In this context, our recently established notion of plasmon coherence engineering enables one to design polychromatic, complex-structured SPP fields of controlled state of coherence, endowed with nontrivial and flexible intensity, polarization, energy flow, and angular momentum distributions. The research in this emerging branch of nanophotonics – statistical plasmonics – is operated in close collaboration with Dalhousie University (Canada) and Soochow University (China).

Contact persons:
Asst. Prof. Andreas Norrman
Prof. Tero Setälä
Prof. Ari T. Friberg

1. A. Norrman, T. Setälä, and A. T. Friberg, “Partial spatial coherence and partial polarization in random evanescent fields on lossless interfaces”, J. Opt. Soc. Am. A 28, 391 (2011).
2. A. Norrman, T. Setälä, and A. T. Friberg, “Partial coherence and polarization of a two-mode surface-plasmon polariton field at a metallic nanoslab”, Opt. Express 23, 20696 (2015).
3. A. Norrman, T. Setälä, and A. T. Friberg, “Generation and electromagnetic coherence of unpolarized three-component light fields”, Opt. Lett. 40, 5216 (2015).
4. A. Norrman, S. A. Ponomarenko, and A. T. Friberg, “Partially coherent surface plasmon polaritons”, EPL 116, 64001 (2016).
5. Y. Chen, A. Norrman, S. A. Ponomarenko, and A. T. Friberg, “Plasmon coherence determination from nanoscattering”, Opt. Lett. 42, 3279 (2017).
6. Y. Chen, A. Norrman, S. A. Ponomarenko, and A. T. Friberg, “Partially coherent axiconic surface plasmon polariton fields”, Phys. Rev. A 97, 041801(R) (2018).
7. Y. Chen, A. Norrman, S. A. Ponomarenko, and A. T. Friberg, “Coherence lattices in surface plasmon polariton fields”, Opt. Lett. 43, 3429 (2018).
8. Y. Chen, A. Norrman, S. A. Ponomarenko, and A. T. Friberg, “Partially coherent surface plasmon polariton vortex fields”, Phys. Rev. A 100, 053833 (2019).
9. Y. Chen, A. Norrman, S. A. Ponomarenko, and A. T. Friberg, “Optical coherence and electromagnetic surface waves” (invited review), Prog. Optics 65, 105 (2020).
10. Y. Chen, A. Norrman, S. A. Ponomarenko, and A. T. Friberg, “Spin density in partially coherent surface-plasmon-polariton vortex fields”, Phys. Rev. A 103, 063511 (2021).

Nanoprobe measurements: Characterization of highly nonparaxial fields is vital in many situations of nanophotonics but for which the traditional beam-field methods are not applicable. A route to extract information of such fields is to employ scattering nanoparticles to mediate local information at the particles to the far-zone where the traditional methods can be used. This resembles the idea of scanning near-field optical microscopy (SNOM) where the near-field intensity is usually of interest. Our goal instead is to measure the polarization and coherence properties of light fields by using nanoscatterers. Earlier we have demonstrated polarization-state detection with a single scatterer and very recently the probing of spatial coherence using two particles in the contexts of both scalar and vectorial light beams. Currently, we are developing nanoprobe measurement techniques for completely general three-component fields.

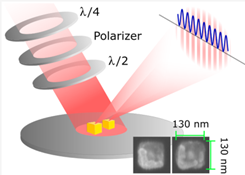
Principle of a nanoscattering measurement of spatial (two-point) coherence (from [3]).

Contact persons:
Asst. Prof. Andreas Norrman
Prof. Tero Setälä
Prof. Ari T. Friberg

1. L.-P. Leppänen, K. Saastamoinen, J. Lehtolahti, A. T. Friberg, and T. Setälä, “Detection of partial polarization of light beams with dipolar nanocubes”, Opt. Express 24, 1472 (2016).
2. K. Saastamoinen, L.-P. Leppänen, I. Vartiainen, A. T. Friberg, and T. Setälä, “Spatial coherence of light measured by nanoscattering”, Optica 5, 67 (2018).
3. K. Saastamoinen, H. Partanen, A. T. Friberg, and T. Setälä, “Probing the electromagnetic degree of coherence of light beams with nanoscatterers”, ACS Photonics 7, 1030 (2020).

 

Vector-field coherence: The foundations of coherence theory of random vectorial light fields and the development of various interferometric schemes to measure such vector-light coherence form a long-standing, major research theme at our center. Over the years we have extended several results of scalar light fields into the domain of electromagnetic optics providing new insights into the physical interpretation of coherence in vectorial light beams and its interplay with the polarization characteristics. Among the most important results is the consistent formulation of the degree of coherence for vector-light fields and the measurement of the so-called polarization time in terms of two photon absorption. Very recent steps include, e.g., the development of ghost polarimetry and phase-contrast imaging, as well as the introduction of new techniques for measuring spectral and temporal coherence in stationary light. This subtopic contains collaboration with the University of Miami (USA), University of Groningen (The Netherlands), Technical University of Darmstadt (Germany), Tampere University (Finland), and Aalto University (Finland).

Left: Illustration of the polarization-state evolution on the Poincarè sphere and the polarization-sensitive Michelson interferometer employed in the measurement of polarization time in terms of two-photon absorption (from [2]). Right: Setup for measuring the spectral coherence Stokes parameters of a partially polarized light beam (from [5], cover picture).

Geometric phase: The Pancharatnam-Berry phase is an additional phase contribution that a light beam acquires when its polarization state undergoes a cyclic in-phase evolution. Besides of its fundamental importance in optics and physics in general, the functionality of some novel optical elements is based on its emergence. Such elements can perform, e.g., focusing of light beams and more sophisticated operations such as generation of various helical beams by utilizing a form of spin-orbit coupling. In our works, we have demonstrated theoretically and experimentally that the geometric phase appears also in both spatial and temporal interference patterns of vectorial beams with different polarization states. This is a completely new context for the geometric phase and its consideration is expected to be important in controlled two-beam interference. This topic contains collaboration with Aalto University (Finland).

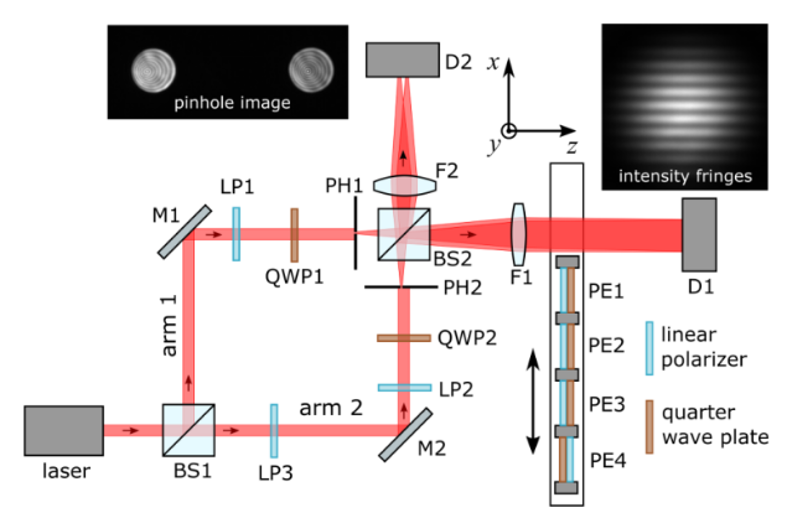
Experimental setup used for studying the geometric phase in Young’s two-pinhole interference (from [1]).

Contact persons:
Dr. Atri Halder
Dr. Kimmo Saastamoinen
Asst. Prof. Andreas Norrman
Assoc. Prof. Tommi Hakala
Prof. Tero Setälä
Prof. Ari T. Friberg

1. A. T. Friberg and T. Setälä, “Electromagnetic theory of optical coherence [Invited]”, J. Opt. Soc. Am. A 33, 2431 (2016).
2. A. Shevchenko, M. Roussey, A. T. Friberg, and T. Setälä, “Polarization time of unpolarized light”, Optica 4, 64 (2017).
3. H. Partanen, B. J. Hoenders, A. T. Friberg, and T. Setälä, “Young’s interference experiment with electromagnetic narrowband light”, J. Opt. Soc. Am. A 35, 1379 (2018); “Editor’s pick”.
4. A. Hannonen, B. J. Hoenders, W. Elsässer, A. T. Friberg, and T. Setälä, “Ghost polarimetry using Stokes correlations”, J. Opt. Soc. Am. A 37, 714 (2020).
5. A. Hannonen, A. Shevchenko, A. T. Friberg, and T. Setälä, “Temporal phase-contrast ghost imaging”, Phys. Rev. A 102, 063524 (2020).
6. H. Partanen, A. T. Friberg, T. Setälä, and J. Turunen, “Spectral measurement of coherence Stokes parameters of random light beams”, Phot. Res. 7, 669 (2019). Cover article of Vol. 7, Issue 6, June 2019.
7. A. Hannonen, H. Partanen, J. Tervo, T. Setälä, and A. T. Friberg, “Pancharatnam-Berry phase in electromagnetic double-pinhole interference”, Phys. Rev. A 99, 053826 (2019).
8. A. Hannonen, K. Saastamoinen, L.-P. Leppänen, M. Koivurova, A. Shevchenko, A. T. Friberg, and T. Setälä, “Pancharatnam-Berry phase in polarization beating of optical beams”, New J. Phys. 21, 083030 (2019).
9. A. Halder, H. Partanen, A. Leinonen, M. Koivurova, T. K. Hakala, T. Setälä, J. Turunen, and A. T. Friberg, “Mirror-based scanning wavefront-folding interferometer for universal coherence measurements”, Opt. Lett. 45, 4260 (2020).
10. A. Hannonen, H. Partanen, A. Leinonen, J. Heikkinen, T. K. Hakala, A. T. Friberg, and T. Setälä, “Measurement of the Pancharatnam-Berry phase in two-beam interference”, Optica 7, 1435 (2020).
11. J. Laatikainen, A. T. Friberg, O. Korotkova, and T. Setälä, “Poincaré sphere of electromagnetic spatial coherence”, Opt. Lett. 46, 2143 (2021).
12. A. Halder, A. Norrman, and A. T. Friberg, “Poincaré sphere representation of scalar two-beam interference under spatial unitary transformations”, Opt. Lett. 46, 5619 (2021).

Our recent efforts focus on combining our expertise and recent findings in contexts of lasing in nanophotonic lattices, geometry, and topology. We aim to realize coherent nanoscale light sources with novel topological properties. The goal is to establish a thorough, solid connection between three crucial concepts, namely 1) the geometry of the lattice 2) the related topology, and 3) polarization and topological properties of the produced coherent nanoscale light fields. The project has the potential to provide fundamental understanding on the topology of nanoscale lasing phenomena, and, in the long term, to provide technological applications.

In addition to various connections in Finland, the research contains collaboration with the Fudan University (China) as well as Iowa State University/Ames Laboratory (USA).

Topologically non-trivial lasing signal from a plasmonic lattice has been recently realized in our experiments [1].

Contact person:
Assoc. Prof. Tommi Hakala

References

1. B. O. Asamoah, M. Necada, W, Liu, J. Heikkinen, S. Mohamed, A. Halder, H. Rekola, M. Koivurova, A. I. Väkeväinen, P. Törmä, J. Turunen, T. Setälä, A. T. Friberg, L. Shi, and T. K. Hakala, “Transition from bright mode to bound state in continuum lasing in plasmonic lattices”, submitted.
2. S. Mohamed, J Wang, H. Rekola, J. Heikkinen, B. O. Asamoah, L. Shi, and T. K. Hakala, “Controlling topology and polarization state of lasing photonic bound states in continuum”, accepted for publication in Laser Photonics Rev., (2022).
3. R. Heilmann, G. Salerno, J. Cuerda, T. K. Hakala, and P. Törmä, “Quasi-BIC mode lasing in a quadrumer plasmonic lattice”, ACS Photonics 9, 224 (2022).
4. S. Droulias, S. Mohamed, H. Rekola, T. K. Hakala, C. M. Soukoulis, and T. Koschny, “Experimental demonstration of dark-state metasurface laser with controllable radiative coupling”, accepted for publication in Adv. Opt. Mater. (2022).